we can calculate the expected rate of return and evaluate the uncertainty, or risk, of an investment by identifying the range of possible returns from that investment and assigning each possible return a weight based on the probability that it will occur. Although the graphs help us visualize the dispersion of possible returns, most investors want to quantify this dispersion using statistical techniques. These statistical measures allow you to compare the return and risk measures for alternative investments directly. Two possible measures of risk (uncertainty) have received support in theoretical work on portfolio theory: the variance and the standard deviation of the estimated distribution of expected returns. In this section, we'll demonstrate how variance and standard deviation measure the dispersion of possible rates of return around the expected rate of return. The formula for variance is as follows:
Variance The larger the variance for an expected rate of return, the greater the dispersion of
expected returns and the greater the uncertainty, or risk, of the investment. The variance for
the perfect-certainty (risk-free) example would be:
Note that, in perfect certainty, there is no variance of return because there is no deviation from expectations and, therefore, no risk or uncertainty. The variance for the second example would be:
The standard deviation is the square root of the variance:
For the second example, the standard deviation would be:
Therefore, when describing this investment example, you would contend that you expect a return of 7 percent, but the standard deviation of your expectations is 11.87 percent.
Relative Measure of Risk
In some cases, an unadjusted variance or standard deviation
can be misleading. If conditions for two or more investment alternatives are not similar—that is, if there are major differences in the expected rates of return—it is necessary to use a measure of relative variability to indicate risk per unit of expected return. A widely used relative measure of risk is the coefficient of variation (CV), calculated as follows:
The CV for the preceding example would be:
Comparing absolute measures of risk, investment B appears to be riskier because it has a standard deviation of 7 percent versus 5 percent for investment A. In contrast, the CV figures show that investment B has less relative variability or lower risk per unit of expected return because it has a substantially higher expected rate of return:
.png)
.png)
.png)
.png)
.png)
.png)

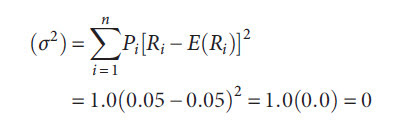







.png)
.png)

.png)
